NBER WORKING PAPER SERIES
DIFFERENCE-IN-DIFFERENCES WITH VARIATION IN TREATMENT TIMING
Andrew Goodman-Bacon
Working Paper 25018
http://www.nber.org/papers/w25018
NATIONAL BUREAU OF ECONOMIC RESEARCH
1050 Massachusetts Avenue
Cambridge, MA 02138
September 2018
I thank Michael Anderson, Martha Bailey, Marianne Bitler, Brantly Callaway, Kitt Carpenter,
Eric Chyn, Bill Collins, John DiNardo, Andrew Dustan, Federico Gutierrez, Brian Kovak, Emily
Lawler, Doug Miller, Sayeh Nikpay, Pedro Sant’Anna, Jesse Shapiro, Gary Solon, Isaac Sorkin,
Sarah West, and seminar participants at the Southern Economics Association, ASHEcon 2018,
the University of California, Davis, University of Kentucky, University of Memphis, University
of North Carolina Charlotte, the University of Pennsylvania, and Vanderbilt University. All errors
are my own. The views expressed herein are those of the author and do not necessarily reflect the
views of the National Bureau of Economic Research.
NBER working papers are circulated for discussion and comment purposes. They have not been
peer-reviewed or been subject to the review by the NBER Board of Directors that accompanies
official NBER publications.
© 2018 by Andrew Goodman-Bacon. All rights reserved. Short sections of text, not to exceed
two paragraphs, may be quoted without explicit permission provided that full credit, including ©
notice, is given to the source.

Difference-in-Differences with Variation in Treatment Timing
Andrew Goodman-Bacon
NBER Working Paper No. 25018
September 2018
JEL No. C1,C23
ABSTRACT
The canonical difference-in-differences (DD) model contains two time periods, “pre” and “post”,
and two groups, “treatment” and “control”. Most DD applications, however, exploit variation
across groups of units that receive treatment at different times. This paper derives an expression
for this general DD estimator, and shows that it is a weighted average of all possible two-group/
two-period DD estimators in the data. This result provides detailed guidance about how to use
regression DD in practice. I define the DD estimand and show how it averages treatment effect
heterogeneity and that it is biased when effects change over time. I propose a new balance test
derived from a unified definition of common trends. I show how to decompose the difference
between two specifications, and I apply it to models that drop untreated units, weight,
disaggregate time fixed effects, control for unit-specific time trends, or exploit a third difference.
Andrew Goodman-Bacon
Department of Economics
Vanderbilt University
2301 Vanderbilt Place
Nashville, TN 37235-1819
and NBER
A data appendix is available at http://www.nber.org/data-appendix/w25018

1
Difference-in-differences (DD) is both the most common and the oldest quasi-experimental
research design, dating back to Snow’s (1855) analysis of a London cholera outbreak.
1
A DD
estimate is the difference between the change in outcomes before and after a treatment (difference
one) in a treatment versus control group (difference two):
. That simple quantity also equals the estimated coefficient on the interaction of a
treatment group dummy and a post-treatment period dummy in the following regression:
= +
+
+
×
+
(1)
The elegance of DD makes it clear which comparisons generate the estimate, what leads to bias,
and how to test the design. The expression in terms of sample means connects the regression to
potential outcomes and shows that, under a common trends assumption, a two-group/two-period
(2x2) DD identifies the average treatment effect on the treated. All econometrics textbooks and
survey articles describe this structure,
2
and recent methodological extensions build on it.
3
Most DD applications diverge from this 2x2 set up though because treatments usually occur
at different times.
4
The processes that generate treatment variables naturally lead to variation in
timing. Local governments change policy. Jurisdictions hand down legal rulings. Natural disasters
strike across seasons. Firms lay off workers. In this case researchers estimate a regression with
dummies for cross-sectional units (
) and time periods (
), and a treatment dummy (
):
=
+
+
+
(2)
1
A search from 2012 forward of nber.org, for example, yields 430 results for “difference-in-differences", 360 for
“randomization” AND “experiment” AND “trial”, and 277 for “regression discontinuity” OR “regression kink”.
2
This includes, but is not limited to, Angrist and Krueger (1999), Angrist and Pischke (2009), Heckman, Lalonde,
and Smith (1999), Meyer (1995), Cameron and Trivedi (2005), Wooldridge (2010).
3
Inverse propensity score reweighting: Abadie (2005), synthetic control: Abadie, Diamond, and Hainmueller (2010),
changes-in-changes: Athey and Imbens (2006), quantile treatment effects: Callaway, Li, and Oka (forthcoming).
4
Half of the 93 DD papers published in 2014/2015 in 5 general interest or field journals had variation in timing.

2
In contrast to our substantial understanding of the canonical 2x2 DD model, we know
relatively little about the two-way fixed effects DD model when treatment timing varies. We do
not know precisely how it compares mean outcomes across groups.
5
We typically rely on general
descriptions of the identifying assumption like “interventions must be as good as random,
conditional on time and group fixed effects” (Bertrand, Duflo, and Mullainathan 2004, p. 250),
and consequently lack well-defined strategies to test the validity of the DD design with timing. We
have limited understanding of the treatment effect parameter that regression DD identifies. Finally,
we often cannot evaluate when alternative specifications will work or why they change estimates.
6
This paper shows that the two-way fixed effects DD estimator in (2) is a weighted average
of all possible 2x2 DD estimators that compare timing groups to each other. Some use units treated
at a particular time as the treatment group and untreated units as the control group. Some compare
units treated at two different times, using the later group as a control before its treatment begins
and then the earlier group as a control after its treatment begins. As in any least squares estimator,
the weights on the 2x2 DD’s are proportional to group sizes and the variance of the treatment
dummy within each pair. Treatment variance is highest for groups treated in the middle of the
panel and lowest for groups treated at the extremes. This result clarifies the theoretical
interpretation and identifying assumptions of the general DD model and creates simple new tools
for describing the design and analyzing problems that arise in practice.
By decomposing the DD estimator into its sources of variation (the 2x2 DD’s) and
providing an explicit interpretation of the weights in terms of treatment variances, my results
5
Imai, Kim, and Wang (2018) note “It is well known that the standard DiD estimator is numerically equivalent to the
linear two-way fixed effects regression estimator if there are two time periods and the treatment is administered to
some units only in the second time period. Unfortunately, this equivalence result does not generalize to the multi-
period DiD design…Nevertheless, researchers often motivate the use of the two-way fixed effects estimator by
referring to the DiD design (e.g., Angrist and Pischke, 2009).”
6
This often leads to sharp disagreements. See Neumark, Salas, and Wascher (2014) on unit-specific linear trends, Lee
and Solon (2011) on weighting and outcome transformations, and Shore-Sheppard (2009) on age time fixed effects.

3
extend recent research on DD models with heterogeneous effects.
7
Assuming equal counterfactual
trends, Abraham and Sun (2018), Borusyak and Jaravel (2017), and de Chaisemartin and
D’HaultfŒuille (2018b) show that two-way fixed effects DD yields an average of treatment effects
across all groups and times, some of which may have negative weights. My results show how these
weights arise from differences in timing and thus treatment variances, facilitating a connection
between models of treatment allocation and the interpretation of DD estimates.
8
I also explain why
the negative weights occur: when already-treated units act as controls, changes in their treatment
effects over time get subtracted from the DD estimate. This negative weighting only arises when
treatment effects vary over time, in which case it typically biases regression DD estimates away
from the sign of the true treatment effect. This does not imply a failure of the underlying design,
but it does caution against the use of a single-coefficient two-way fixed effects specification to
summarize time-varying effects.
I also show that because regression DD uses group sizes and treatment variances to weight
up simple estimates that each rely on common trends between two groups, its identifying
assumption is a variance-weighted version of common trends between all groups. The extent to
which a group’s differential trend biases the overall estimate equals the difference between how
much weight it gets when it acts as the treatment group and how much weight it gets when it acts
as the control group. When the earliest and/or latest treated units have low treatment variance, they
can get more weight as controls than treatments. In designs without untreated units they always
7
Early research in this area made specific observations about stylized specifications such as models with no unit fixed
effects (Bitler, Gelbach, and Hoynes 2003), or it provided simulation evidence (Meer and West 2013).
8
Related results on the weighting of heterogeneous treatment effects does not provide this intuition. Abraham and
Sun (2018, p 9) describe the weights in a DD estimate with constant treatment effects as “residual[s] from predicting
treatment status,
,
with unit and time fixed effects.” de Chaisemartin and D’HaultfŒuille (2018b, p 7) and Borusyak
and Jaravel (2017) describe these same weights as coming from an auxiliary regression and Borusyak and Jaravel
(2017, p 10-11) note that “a general characterization of [the weights] does not seem feasible.” Athey and Imbens
(2018) also decompose the DD estimator and develop design-based inference methods for this setting. Strezhnev
(2018) expresses
as an unweighted average of DD-type terms across pairs of observations and periods.
4
do. These weights, derived from the estimator itself, form the basis of a new balance test that
generalizes the traditional notion of balance between treatment and control groups, and improves
on existing strategies that test between treated/untreated units or early/later treated units.
Finally, I use the weighted average result to develop simple tools to describe the general
DD design and evaluate why estimates change across specifications. Simply plotting the 2x2 DD’s
against their weight displays heterogeneity in the estimated components and shows which terms
or groups matter most. Summing the weights on the timing comparisons versus treated/untreated
comparisons quantifies “how much” of the variation comes from timing (a common question in
practice). Additionally, the difference between DD estimates across specifications can often be
written as a Oaxaca-Blinder-Kitagawa style decomposition allowing researchers to calculate how
much comes from the 2x2 DD’s, the weights, or the interaction of the two. The source of instability
matters because changes due to different weighting reflect changes in the estimand (not bias),
while changes in the 2x2 DD’s suggest that covariates address confounding. Scatter plots of the
2x2 DD’s (or the weights) from different specifications show which specific terms drive these
differences. I develop this approach for models that weight, use triple-differences, control for unit-
specific time trends (or pre-trends only), and control for disaggregated time fixed effects.
To demonstrate these methods I replicate Stevenson and Wolfers (2006) two-way fixed
effects DD study of the effect of unilateral divorce laws on female suicide rates. The two-way
fixed effects model suggest that unilateral divorce leads to 3 fewer suicides per million women.
More than a third of the identifying variation comes from treatment timing and the rest comes from
comparisons to states with no reforms during the sample period. Event-study estimates show that
the treatment effects vary strongly over time, however, which biases many of the timing
comparisons. The DD estimate (-3.08) is therefore a misleading summary estimate of the average

5
post-treatment effect, which is closer to -5. My proposed balance test detects significantly higher
per-capita income and male/female sex ratios in reform states, in contrast to joint tests of covariate
balance across timing groups, which cannot reject the null of balance. Finally, my results show
that much of the sensitivity across specifications comes from changes in weights, or a small
number of 2x2 DD’s, and need not indicate bias.
I. THE DIFFERENCE-IN-DIFFERENCES DECOMPOSITION THEOREM
When units experience treatment at different times, one cannot estimate equation (1) because the
post-period dummy is not defined for control observations. Nearly all work that exploits variation
in treatment timing uses the two-way fixed effects model in equation (2) (Cameron and Trivedi
2005 pg. 738). Researchers clearly recognize that differences in when units received treatment
contribute to identification, but have not been able to describe how these comparisons are made.
9
The simplest way to illustrate how treatment timing works is to consider a balanced panel
dataset with periods () and cross-sectional units () that belong to either an untreated group,
; an early treatment group, , which receives a binary treatment at
; and a late treatment group,
, which receives the binary treatment at
>
. Figure 1 plots this structure.
Throughout the paper I use “group” or “timing group” to refer to collections of units either
treated at the same time or not treated. I refer to units that do not receive treatment as “untreated”
rather than “control” units because, while they obviously act as controls, treated units do, too.
will denote an earlier treated group and will denote a later treated group. Each group’s sample
share is
and the share of time it spends treated is
. I use
()
to denote the sample mean
of
for units in group during group ’s post period,
[
,
]
. (
()
is defined similarly.)
9
Angrist and Pischke (2015), for example, lay out the canonical DD model in terms of means, but discuss regression
DD with timing in general terms only, noting that there is “more than one…experiment” in this setting.

6
The challenge in this setting has been to articulate how estimates of equation (2) compare
the groups and times depicted in figure 1. We do, however, have clear intuition, for 2x2 designs in
which one group’s treatment status changes and another’s does not. We could form several such
designs, estimable by equation (1), in the three-group case. Figure 2 plots them.
Panels A and B show that with only one of the two treatment groups, an estimate from
equation (2) reduces to the canonical case comparing a treated to an untreated group:
(
)
(
)
(
)
(
)
, = , . (3)
If instead there were no untreated units, the two way fixed effects estimator would be identified
only by the differential treatment timing between groups and . For this case, panels C and D
plot two clear 2x2 DD’s based on sub-periods when only one group’s treatment status changes.
Before
, the early units act as the treatment group because their treatment status changes, and
later units act as controls during their pre-period. We compare outcomes between the window
when treatment status varies, (, ), and group ’s pre-period,
(
)
:
,
(
,
)
(
)
(
,
)
(
)
(4)
The opposite situation, shown in panel D, arises after
when the later group changes treatment
status but the early group does not. Later units act as the treatment group, early units act as controls,
and we compare average outcomes between the periods
(
)
and
(
,
)
:
,
(
)
(
,
)
(
)
(
,
)
(5)
The already-treated units in group can serve as controls even though they are treated because
treatment status does not change.
My central result is that any two-way fixed effects DD estimator is a weighted average of
well-understood 2x2 DD estimators, like those plotted in figure 2. To see why, first assume a

7
balanced panel and partial out unit and time fixed effects from
and
using the Frisch-Waugh
theorem (Frisch and Waugh 1933). Denote grand means by =
, and adjusted
variables by
= (
) (
) (
).
then equals the univariate regression
coefficient between adjusted outcome and treatment variables:
(
,
)
(
)
=
1
1
The numerator equals the sample covariance between
and
minus the sample covariances
between unit means and between time means:
(
,
) =
1
(
)(
)
1
(
)(
)
1
(
)(
)
(6)
The appendix shows how to simplify this covariance using the binary nature of
, and by
replacing the
and
terms with weighted averages of pre- and post-treatment means or means
in each group.
10
This gives the following theorem:
Theorem 1. Difference-in-Differences Decomposition Theorem
Assume that the data contain = 1, . . . , groups of units ordered by the time when they receive
a binary treatment,
(1, ]. There may be one group, , that never receives treatment. The
OLS estimate,
, in a two-way fixed-effects model (2) is a weighted average of all possible two-
by-two DD estimators.
=
+
[
,
+ (1
)
,
]
(7)
Where the two-by-two DD estimators are:
(
)
(
)
(
)
(
)
10
Note that the first two terms in equation (6) collapse to a function of pre/post mean differences because
=
=
0 in the untreated group,
= 0 in pre-treatment periods, and
=
()
(1
)
()
. The sums over
thus include only the treated units and the sum over includes only post-periods (>
). Similarly, sum over time
can be broken into pieces based on the different groups’ treatment times, and the time means of
weight together
each group’s mean.
(
) follows from replacing
with
in the expression for
(
,
).

8
,
(
,
)
(
)
(
,
)
(
)
,
(
)
(
,
)
(
)
(
,
)
the weights are:
=
(1
)
(
)
=
(
)(1 (
))
(
)
=
1
1 (
)
and
+
= 1.
Proof: See appendix A.
Theorem 1 completely describes the sources of identifying variation in a general DD model
and their importance. With timing groups, one could form
“timing-only” estimates that
either compare an earlier- to a later-treated timing group (
,
) or a later- to earlier-treated timing
group (
,
). With an untreated group, one could form 2x2 DD’s that compare each timing
group to the untreated group (
). Therefore, with timing groups and one untreated group, the
DD estimator comes from
distinct 2x2 DDs.
The weights come both from group sizes, via the
’s, and the treatment variance in each
pair.
11
With one treated group, the variance of the treatment dummy is
(1
), and is highest
11
Many other least-squares estimators weight heterogeneity this way. A univariate regression coefficient equals an
average of coefficients in mutually exclusive (and demeaned) subsamples weighted by size and the subsample -
variance:
=
(
)(
)
(
)
=
(
)() +
(
)()
(
)
=
+
=
,
+
,
Similarly, the Wald/IV theorem (Angrist 1988) shows that any IV estimate is a linear combination of Wald estimators
that compare two values of the instrument. Gibbons, Serrato, and Urbancic (2018) show a nearly identical weighting
formula for one-way fixed effects. Panel data provide another well-known example: a pooled regression coefficients
equals a variance-weighted average of two distinct estimators that each use less information: the between estimator
for subsample means, and the within estimator for deviations from subsample means.

9
for units treated in the middle of the panel with
= 0.5. With two treated groups, the variance
of the difference in treatment dummies is (
)(1 (
)), and is highest for pairs
whose treatment shares differ by 0.5. Figure 2 sets
and
so that
= 0.67 and
= 0.15,
which means that
(
1
)
= 0.22 > 0.13 =
(
1
)
. Because it has higher treatment
variance, group ’s comparison to the untreated group,
, gets more weight (
= 0.365) than
the corresponding term for group ,
(
= 0.202). The difference in treated shares is
= 0.52, so
= 0.412.
12
This decomposition theorem also shows how DD compares groups treated at different
times. A two-group “timing-only” estimator is itself a weighted average of the 2x2 DD’s plotted
in panels C and D of figure 2:
,
+ (1
)
,
(8)
Both groups serve as controls for each other during periods when their treatment status does not
change, and the group with higher treatment variance (that is, treated closer to the middle the panel)
gets more weight. In the three group example
(
1
)
>
(
1
)
so
= .67.
Multiplying this by
= 0.412, shows that
,
gets less weight than
,
:
(
1
)
=
0.135 < 0.278 =
.
13
12
Changing the number or spacing of time periods changes the weights. Imagine adding periods to the end of the
three-group panel. This would reduce
(
)
to 0.835
(
1 0.835
)
= 0.138, but it would increase
(
)
to
0.58
(
1 0.58
)
= 0.244. This puts less weight on terms where is the treatment group (
= 0.24 and
=
0.07) and more weight on terms where is the treatment group (
= 0.43 and
(
1
)
= 0.26).
13
Two recent papers present clear analyses using two-group timing-only estimators. Malkova (2017) studies a
maternity benefit policy in the Soviet Union and Goodman (2017) studies high school math mandates. Both papers
show differences between early and late groups before the reform,
(),
during the period when treatment status
differs,
(,
), and in the period after both have implemented reforms,
(
).
10
II. THEORY: WHAT PARAMETER DOES DD IDENTIFY AND UNDER WHAT ASSUMPTIONS?
Theorem 1 relates the regression DD coefficient to sample averages, which makes it simple to
analyze its statistical properties by writing
in terms of potential outcomes (Holland 1986,
Rubin 1974). The outcome is
=
+
(
1
)
, where
is unit ’s treated outcome at
time , and
is the corresponding untreated outcome. Following Callaway and Sant'Anna (2018,
p 7) define the ATT for timing group at time (the “group-time average treatment effect”):
(
)
[
, =
]
. Because regression DD averages outcomes in pre- and post-
periods, I define the average of the
(
)
in a date range, :
(
)
[
,
]
(9)
In practice, will represent post-treatment windows that appear in the 2x2 components. Finally,
define the difference over time in average potential outcomes (treated or untreated) as:
(
,
)
,
,
, = 0,1 (10)
Applying this notation to the 2x2 DD’s in equations (3)-(5), adding and subtracting post-period
counterfactual outcomes for the treatment group yields the familiar result that (the probability limit
of) each 2x2 DD equals an ATT plus bias from differential trends:
=
(
()
)
+
(
(), ()
)
(
)
,
(
)
(
11
)
,
=
(
,
)
+
(
(
,
)
, ()
)
(
,
)
,
(
)
(
11
)
,
=
(
()
)
+
(),
(
,
)
(
)
,
(
,
)
(
)
(
,
)
(11)
Note that the definition of common trends in (11a) and (11b) involves only counterfactual
outcomes, but in (11c) identification of
(
()
)
involves counterfactual outcomes and
changes in treatment effects in the already-treated “control group”.

11
Substituting equations (11a)-(11c) into the DD decomposition theorem expresses the
probability limit of the two-way fixed effects DD estimator (assuming that is fixed and grows)
in terms of potential outcomes and separates the estimand from the identifying assumptions:
=
= + + (12)
The first term in (12) is the two-way fixed effects DD estimand, which I call the “variance-
weighted average treatment effect on the treated” (VWATT):
(
)
+
(
,
)
+
(
1
)
(
)
(12)
The terms correspond to the terms in equation (7), but replace sample shares () with
population shares (
).
14
VWATT is always a positively weighted average of ATTs for the units
and periods that act as treatment groups across the 2x2 DD’s that make up
. The weights come
from the decomposition theorem and reflect group size and treatment variance.
The second term, which I call “variance-weighted common trends” (VWCT) generalizes
common trends to a setting with timing variation:
(
)
,
(
)
(
)
,
(
)
+
(
,
)
,
(
)
(
,
)
,
(
)
+
(
1
)
(
)
,
(
,
)
(
)
,
(
,
)
(12)
14
Note that a DD estimator is not consistent if gets large because the permanently turned on treatment dummy
becomes collinear with the unit fixed effects (
does not converge to a positive definite matrix). Asymptotics with
respect to require the time dimension to grow in both directions (see Perron 2006).

12
Like VWATT, VWCT is also an average of the difference in untreated potential outcome trends
between pair of groups (and over different time periods) using the weights from the decomposition
theorem. VWCT is new, it defines internal validity for the DD design with timing, and it is weaker
than the more commonly assumed equal counterfactual trends across groups.
The last term in (12) equals a weighted sum of the change in treatment effects within each
unit’s post-period:
(
1
)
(
)
(
,
)
(12)
Because already-treated groups sometimes act as controls, the 2x2 estimators in equation (11c)
subtract average changes in their untreated outcomes and their treatment effects. Equation (12c)
defines the bias that comes from estimating a single-coefficient DD model when treatment effects
vary over time. Note that this does not mean that the DD research design is invalid. In this case
other specifications, such as an event-study model (Jacobson, LaLonde, and Sullivan 1993) or
“stacked DD” (Abraham and Sun 2018, Deshpande and Li 2017, Fadlon and Nielsen 2015), or
other estimators such as reweighting strategies (Callaway and Sant'Anna 2018, de Chaisemartin
and D’HaultfŒuille 2018b) may be more appropriate.
Recent DD research comes to related conclusions about DD models with timing, but does not
describe the full estimator as in equation (12). Abraham and Sun (2018), Borusyak and Jaravel
(2017), and de Chaisemartin and D’HaultfŒuille (2018b) begin by imposing pairwise common
trends (VWCT=0), and then incorporating into the DD estimand.
15
The structure of the
decomposition theorem, however, suggests that we should think of as a source of bias
15
Abraham and Sun (2018, p 6) assume “parallel trends in baseline outcome”; Borusyak and Jaravel (2017, p 10)
assume “no pre-trends”; and de Chaisemartin and D’HaultfŒuille (2018b, p 6) assume “common trends” in
counterfactual outcomes. Two of these papers analyze common specifications that I do not consider. de Chaisemartin
and D’HaultfŒuille (2018b) discuss designs where treatment evolves continuously within group-by-time cells and
first-difference specifications. Abraham and Sun (2018) analyze the estimand for semi-parametric event-study models.

13
because it arises from the way equation (2) forms “the” control group. This distinction, made clear
in equation (12), ensures an interpretable estimand (VWATT) and clearly defined identifying
assumptions.
16
This follows from at least two related precedents. de Chaisemartin and
D’HaultfŒuille (2018a, p. 5) prove identification of dose-response DD models under the
assumption that “the average effect of going from 0 to d units of treatment among units with
D(0)=d is stable over time.” Treatment effect homogeneity ensures an estimand with no negative
weights. Similarly, the monotonicity assumption in Imbens and Angrist (1994) ensures that the
local average treatment effect does not have negative weights. In other words, negative weights
are a failure of identification rather than a feature of the IV estimand.
A. Interpreting the DD Estimand
When the treatment effect is a constant,
(
)
= , = 0, and = . The
rest of this section assumes that VWCT=0 and discusses how to interpret VWATT under different
forms of treatment effect heterogeneity.
i. Effects that vary across units but not over time
If treatment effects are constant over time but vary across units, then
(
)
=
and we
still have = 0. In this case DD identifies:
=
+
(1
) +
(13)
16
Equation (12) shows that the negative weighting pointed out elsewhere only occurs when treatment effects vary
over time. The mapping between (12) and existing decompositions can be made explicit by rewriting all the
(
)
terms (see equation 9) in terms of group-time effects, which are the object of, for example, Theorem 1 in de
Chaisemartin and D’HaultfŒuille (2018b). In general, each group-time effect receives a total amount of weight that
comes partly from strictly positive terms (equation 12b) and some from potentially negative terms (equation 12c).
When treatment effects are constant, though, the negative weights in (12c) on the group-time effects in
(
,
)
can
cel with the positive weights on group-time effects in
(
)
.
Then = 0 and
DD estimates VWATT, which has strictly positive weights.

14
VWATT weights together the group-specific ATTs not by sample shares, but by a function of
sample shares and treatment variance. The weights in (13) equal the sum of the decomposition
weights for all the terms in which group acts as the treatment group, defined as
.
The parameter in (13) does not necessarily have a structural interpretation. In general,
, so the parameter does not equal the sample ATT.
17
Neither are the weights proportional
to the share of time each unit spends under treatment, so VWATT also does not equal the effect in
the average treated period. The weights, specifically the central role of treatment variance, comes
from the use of least squares. OLS combines 2x2 DD’s efficiently by weighting them according
to variances of the treatment dummy.
18
VWATT lies along the bias/variance tradeoff: the weights
deliver efficiency by potentially moving the point estimate away from, say, the sample ATT.
This tradeoff may not be worthwhile, particularly when VWATT differs strongly from a
given parameter of interest, which occurs when treatment effect heterogeneity is correlated with
treatment timing. Therefore, the processes that determine treatment timing are central to the
interpretation of VWATT (see Besley and Case 2002). For example, a Roy model of selection on
gains (where the number of units treated in each period is constrained) implies that treatment rolls
out first to units with the largest effects. Site selection in experimental evaluations of training
programs (Joseph Hotz, Imbens, and Mortimer 2005) and energy conservation programs (Allcott
2015) matches this pattern. In this case, regression DD underestimates the sample-weighted ATT
if
is early enough (or there are a lot of “post” periods) so that
is very small and
0.5,
and overestimates it if
is late enough (or there are a lot of “pre” periods) so that
0.5 and
17
Abraham and Sun (2018), Borusyak and Jaravel (2017), Chernozhukov et al. (2013), de Chaisemartin and
D’HaultfŒuille (2018b), Gibbons, Serrato, and Urbancic (2018), Wooldridge (2005) all make a similar observation.
The DD decomposition theorem, provides a new solution for the relevant weights.
18
This is exactly analogous to the result that two-stage least squares is the estimator that “efficient combines alternative
Wald estimates” (Angrist 1991).

15
is small. The opposite conclusions follow from “reverse Roy” selection where units with the
smallest effects select into treatment first, which describes the take up of housing vouchers (Chyn
forthcoming) and charter school applications (Walters forthcoming).
An easy way to gauge whether VWATT and a sample-weighted ATT is to scatter the
weights from (13) against each group’s sample share. These two may be close if there is little
variation in treatment timing, if the untreated group is very large, or if some timing groups are very
large. Conversely, weighting matters less if the
’s are similar, which one can evaluate by
aggregating each group’s 2x2 DD estimates from the decomposition theorem.
19
Finally, one could
directly compare VWATT to point estimates of a particular parameter of interest. Several
alternative estimators can deliver differently weighted averages of ATT’s (Abraham and Sun 2018,
Callaway and Sant'Anna 2018, de Chaisemartin and D’HaultfŒuille 2018b).
ii. Effects that vary over time but not across units
Time-varying treatment effects (even if they are identical across units) generate cross-group
heterogeneity in VWATT by averaging time-varying effects over different post-treatment
windows, but more importantly they mean that 0. Equations (11b) and (11c) show that
common trends in counterfactual outcomes leaves one set of timing terms biased (
,
), while
common trends between counterfactual and treated outcomes leaves the other set biased (
,
).
To illustrate this point, figure 3 plots a case where counterfactual outcomes are identical,
but the treatment effect is a linear trend-break,
=
+ (
+ 1) (see Meer and West
2013).
,
uses group as a control group during its pre-period and identifies the ATT during
19
Relatedly, de Chaisemartin and D’HaultfŒuille (2018b) derive a statistic that gives the minimum variation in
treatment effects that could lead to wrong-signed regression estimates when all treatment effects have the same sign.

16
the middle window in which treatment status varies:
.
,
, however, is biased
because the control group () experiences a trend in outcomes due to the treatment effect:
20
,
=
(
()
)
(
)
(
1
)
2
=
(
)
2
0 (14)
This bias feeds through to
according to the size of (1
):
=
[(2
1)(
) + 1]
2
(15)
The entire two-group timing estimate can be wrong signed if
is small (putting more weight on
the downward biased term). In figure 3, for example, both units are treated equally close to the
ends of the panel, so
= 0.5 and the estimated DD effect equals
, even though both units
experience treatment effects as large as [(
1)]. This type of bias affects the overall
DD estimate according to the weights in equation (7). It is smaller when there are untreated units,
more so when these units are large.
Note that this bias is specific to the specification in equation (2). More flexible event-study
specifications may not suffer from this problem (although see Proposition 2 in Abraham and Sun
20
The average of the effects for group during any set of positive event-times is just times the average event-time.
The
(,
) period contains event-times 0 through
1 and the () period contains event-times
(
1) through (
1)), so we have:
(
,
)
=
(
)(
+ 1
)
2
(
)
=
+ 1
2
(
)
=
(
)
+
+ 2
2
And the difference, which appears in the identifying assumption in (11c) equals:
(
)
(
,
)
=
(
)
+
+ 2
2
+ 1
2
=
2
(
1
)
Another way to see this, as noted in figure 3, is that average outcomes in the treatment group are always below average
outcomes in the early group in the
(
) period and the difference equals the maximum size of the treatment effect
in group at the end of the (, ) period: (
+ 1). Average outcomes for the late group are also below
average outcomes in the early group in the
(,
) period, but by the average amount of the treatment effect in
group during the
(,
) period:
(
)
. Outcomes in group actually fall on average relative to group ,
which makes the DD estimate negative even when all treatment effects are positive.

17
2018). Fadlon and Nielsen (2015) and Deshpande and Li (2017) use a novel estimator that matches
treated units with controls that receive treatment a given amount of time later. This specification
does not use already treated units as controls, and yields an average of
,
terms with a fixed
post-period. Callaway and Sant'Anna (2018) discuss how to summarize heterogeneous treatment
effects in this context and develop a reweighting estimator to do so. Summarizing time-varying
effects using equation (2), however, yields estimates that are too small or even wrong-signed, and
should not be used to judge the meaning or plausibility of effect sizes.
21
B. What is the identifying assumption and how should we test it?
The preceding analysis maintained the assumption of equal counterfactual trends across groups,
but (12) shows that (as long as treatment effects do not vary over time) identification of VWATT
only requires VWCT to equal zero. The assumption itself is untestable because we cannot, for
example, observe changes in
that occur after treatment or test for them using pre-treatment
data.
22
Assuming that differential counterfactual trends,
, are linear throughout the panel leads
to a convenient approximation to VWCT:
23
+
(1 2
) +
(2
1)
= 0 (16)
21
Borusyak and Jaravel (2017) show that that common, linear trends, in the post- and pre- periods cannot be estimated
in this design. The decomposition theorem shows why: timing groups act as controls for each other, so permanent
common trends difference out. This is not a meaningful limitation for treatment effect estimation, though, because
“effects” must occur after treatment. Job displacement provides a clear example (Jacobson, LaLonde, and Sullivan
1993, Krolikowski 2017). Comparisons based on displacement timing cannot identify whether all displaced workers
have a permanently different earnings trajectory than never displaced workers (the unidentified linear component),
but they can identify changes in the time-path of earnings around the displacement event (the treatment effect).
22
One can use time-varying confounders as outcomes (Freyaldenhoven, Hansen, and Shapiro 2018, Pei, Pischke, and
Schwandt 2017), but this does not test for balance in levels, nor can it be used for sparsely measured confounders.
23
The path of counterfactual outcomes can affect each 2x2 DD’s bias term in different ways. Linearly trending
unobservables, for example, lead to larger bias in 2x2 DD’s that use more periods. I show in the appendix that in the
linear case differences in the magnitude of the bias cancel out across each group’s “treatment” and “control” terms,
and equation (16) holds.

18
Equation (16) generalizes the definition of common trends and collapses to the typical pairwise
common trends assumption for any two-group estimator. It is immediately clear that identical
trends across all groups satisfies (16), but this is not a necessary condition for it to hold since the
bias induced by a given group’s trend depends on the weights in brackets.
24
Fortunately, the weights have an intuitive interpretation. The weight on each group’s
counterfactual trend equals the difference between the total weight it gets when it acts as a
treatment group—
from equation (13)—minus the total weight it gets when it acts as a control
group—
. can therefore be written as:
[
]
= 0 (17)
Figure 4 plots
as a function of
(assuming equal group sizes). Units treated in the
middle of the panel have high treatment variance and get a lot of weight when they act as the
treatment group, while units treated toward the ends of the panel get relatively more weight when
they act as controls. As
moves closer to 1 or T,
becomes negative, which shows that
some timing groups effectively act as controls. This helps define “the” control group in timing-
only designs (the dashed line in figure 6): all groups are controls in some terms, but the earliest
and/or latest units necessarily get more weight as controls than treatments. The weights also map
differential trends to bias.
25
A positive trend in group induces positive bias when
> 0,
negative bias when
< 0 (that is, if is an effective control group), and no bias when
= 0. The size of the bias from a given trend is larger for groups with more weight.
24
Callaway and Sant'Anna (2018) provide alternative definitions of common trends and tests not based on linearity.
25
Applications typically discuss bias in general terms, arguing that unobservables must be “uncorrelated” with timing,
but have not been able to specify how counterfactual trends would bias a two-way fixed effects estimate. For example,
Almond, Hoynes, and Schanzenbach (2011, p 389-190) argue: “Counties with strong support for the low-income
population (such as northern, urban counties with large populations of poor) may adopt FSP earlier in the period. This
systematic variation in food stamp adoption could lead to spurious estimates of the program impact if those same
county characteristics are associated with differential trends in the outcome variables.”

19
Equation (17) also shows exactly how to weight together averages of
and perform a
single -test that directly captures the identifying assumption. Generate a dummy for the effective
treatment group,
=
> 0, then regress timing-group means,
, on
weighting by
. The coefficient on
equals covariate differences weighted by the actual identifying
variation, and its t-statistic tests the null of reweighted balance in (17). One can also use this
strategy to test for pre-treatment trends in confounders (or the outcome) by regressing
on
,
year dummies, and their interaction, or the interaction of
with a linear trend using dates before
any treatment starts.
26
The reweighted balance test has advantages over other strategies for testing balance in this
setting. Regressing
on a constant and dummies for timing groups allows a test of the null of
joint balance across groups (
:
= 0,). With many timing groups, however, this
F-test will have low power, it does not reflect the importance of each group (
), and does
not show the sign or magnitude of any imbalance.
27
The reweighted test, on the other hand, has
higher power and describes the sign and magnitude of imbalance. It is also better than a test for
linear relationships between
and
or tests for balance between “early” and “late” treated units
(Almond, Hoynes, and Schanzenbach 2011, Bailey and Goodman-Bacon 2015). Because the
effective control group can include both the earliest and latest treated units, failing to find a linear
relationship between
and
can miss the relevant imbalance between the most important
“middle” units and the end points.
26
Plotting confounders or pre-trends across groups, however, is important to ensure that a failure to reject does not
reflect offsetting trends or covariate means across timing groups.
27
Note that using an event-study specification to evaluate pre-trends does not test for joint equality of pre-trends
either. It tests for common trends using the (heretofore unarticulated) estimator itself.

20
III. DD DECOMPOSITION IN PRACTICE: UNILATERAL DIVORCE AND FEMALE SUICIDE
To illustrate how to use DD decomposition theorem in practice, I replicate Stevenson and Wolfers’
(2006) analysis of no-fault divorce reforms and female suicide. Unilateral (or no-fault) divorce
allowed either spouse to end a marriage, redistributing property rights and bargaining power
relative to fault-based divorce regimes. Stevenson and Wolfers exploit “the natural variation
resulting from the different timing of the adoption of unilateral divorce laws” in 37 states from
1969-1985 (see table 1) using the “remaining fourteen states as controls” to evaluate the effect of
these reforms on female suicide rates. Figure 5 replicates their event-study result for female suicide
using an unweighted model with no covariates.
28
Our results match closely: suicide rates display
no clear trend before the implementation of unilateral divorce laws, but begin falling soon after.
They report a DD coefficient in logs of -9.7 (s.e. = 2.3). I find a DD coefficient in levels of -3.08
(s.e. = 1.13), or a proportional reduction of 6 percent.
29
A. Describing the design
Figure 6 uses the DD decomposition theorem to illustrate the sources of variation. I plot each 2x2
DD against its weight and calculate the average effect and total weight for the three types of 2x2
comparisons: treated/untreated, early/late, late/early.
30
As theorem 1 states, the two-way fixed
effects estimate, -3.08, is an average of the y-axis values weighted by their x-axis values. Summing
the weights on timing terms (
) shows exactly how much of
comes from timing variation
(37 percent). The large untreated group puts a lot of weight on
terms, but more on those
28
Data on suicides by age, sex, state, and year come from the National Center for Health Statistics’ Multiple Cause of
Death files from 1964-1996, and population denominators come from the 1960 Census (Haines and ICPSR 2010) and
the Surveillance, Epidemiology, and End Results data (SEER 2013). The outcome is the age-adjusted (using the
national female age distribution in 1964) suicide mortality rate per million women. The average suicide rate in my
data is 52 deaths per million women versus 54 in Stevenson and Wolfers (2006). My replication analysis uses levels
to match their figure, but the conclusions all follow from a log specification as well.
29
The differences in the magnitudes likely come from three sources: age-adjustment (the original paper does not
describe an age-adjusting procedure); data on population denominators; and my omission of Alaska and Hawaii.
30
There are 156 distinct DD components: 12 comparisons between timing groups and pre-reform states, 12
comparisons between timing groups and non-reform states, and
(
12
12
)
/2 = 66 comparisons between an earlier
switcher and a later non-switcher, and 66 comparisons between a later switcher and an earlier non-switcher

21
involving pre-1964 reform states (38.4 percent) than non-reform states (24 percent). Figure 6 also
highlights the role of a few influential 2x2 terms—comparisons between the 1973 states and non-
reform or pre-1964 reform states account for 18 percent of the estimate, and the ten highest-weight
2x2 DD’s account for over half.
The bias resulting from time-varying effects is also apparent in figure 6. The average of
these post-treatment event-study estimates in figure 5 is -4.92, while the DD estimate is just 60
percent as large. The difference stems from the comparisons of later- to earlier-treated groups. The
average treated/untreated estimates are negative (-5.33 and -7.04) as are the comparisons of earlier-
to later-treated states (although less so: -0.19).
31
The comparisons of later- to earlier-treated states,
however, are positive on average (3.51) and account for the bias in the overall DD estimate. Using
the decomposition theorem to take these terms out of the weighted average yields an effect of -
5.44—close to the average of the event-study coefficients. The DD decomposition theorem shows
that one way to summarize effects in the presence of time-varying heterogeneity is simply to
subtract the components of the DD estimate that are biased using the weights in equation (7).
B. Testing the design
Figures 7 and 8 test for covariate balance in the unilateral divorce analysis. Figure 6 plots the
reweighted balance test weights,
, from equation (17), the corresponding weights from a
timing-only design, and each group’s sample share. Larger groups have larger weight, but because
they have relatively low treatment variance, the earliest timing groups are downweighted relative
to their sample shares.
32
In fact, the 1969 states effectively act as controls because
< 0.
31
This point also applies to units that are already treated at the beginning of the panel, like the pre-1964 reform states
in the unilateral divorce analysis. Since their
= 1 they can only act as an already-treated control group. If the
effects for pre-1964 reform states were constant they would not cause bias.
32
Adding 5 × to the suicide rate for the 1970 states (
= 0.0039) changes the DD estimate from -3.08
to -2.75, but adding it to the 1973 group (
= 0.18) yields a very biased DD estimate of 12.28.

22
Figure 8 implements both a joint balance test and the reweighted test using two potential
determinants of marriage market equilibria in 1960: per-capita income and the male/female sex
ratio. Panel A shows that average per-capita income in untreated states ($13,431) is lower than the
average in every timing group except for those that implemented unilateral divorce in 1969 (which
actually get more weight as controls) or 1985. The joint -test, however, fails to reject the null
hypothesis that these means are the same. It is not surprising that such a low power test (12
restrictions on 48 states observations) fails to generate strong evidence against the null. The
reweighed test, on the other hand, does detect a difference in per-capita income of $2,285 between
effective treatment states—those that implemented unilateral divorce in 1970 or later—and
effective control states—pre-1964 reform states, non-reform states, and the 1969 states. Panel B
shows that the 1960 sex ratio is higher in almost all treatment states than in the control states.
While the joint test cannot reject the null of equal means, the reweighted test does reject reweighted
balance (= 0.06).
33
C. Evaluating alternative specifications
Researchers almost always estimate models other than (2) and use differences across specifications
to evaluate internal validity (Oster 2016) or choose projects in the first place. The DD
decomposition theorem suggests a simple way to understand why estimates change. Stacking the
2x2 DD’s and weights from (7) into vectors, we can write
=
. Any alternative
specification that equals a weighted average can be written similarly, and the difference between
33
One can run a joint test of balance across covariates using a seemingly unrelated regressions (SUR), as suggested
by Lee and Lemieux (2010) in the regression discontinuity context. The results of these
2
tests are displayed at the
top of figure 6. As with the separate balance tests, I fail to reject the null of equal means across groups and covariates.
The joint reweighted balance test, however, does reject the null of equal weighted means between effective treatment
and control groups. With 48 states and 12 timing groups, there are not sufficient degrees of freedom to implement a
full joint test across many covariates. This is an additional rationale for the reweighted test.

23
the two estimates has the form of a Oaxaca-Blinder-Kitagawa decomposition (Blinder 1973,
Oaxaca 1973, Kitagawa 1955):
=
+
(
)
+
(
)
(18)
Dividing each term on the right side of (18) by
shows the proportional contribution of
changes in the 2x2 DD’s, changes in the weights, and the interaction of the two.
34
Differences
arising from the 2x2 DD’s show that control variables are correlated with treatment and the
outcome, often pointing to a real sources of bias. Differences arising because of the weights,
though, change the way the DD deals with heterogeneity and do not indicate that the 2x2 DD’s are
confounded. It is also simple to learn which terms drive each kind of difference by plotting
against
and against
. One of the most valuable contributions of the DD decomposition
theorem is to provide simple new tools for learning why estimates change across specifications.
i. Dropping Untreated Units
Papers commonly estimate models with and without untreated units, and the decomposition
theorem shows that this is equivalent to setting all
= 0 and rescaling the
to sum to one.
Table 2 shows that this changes the unilateral divorce estimate so much that it becomes positive
(2.42, s.e. = 1.81), but figure 6 suggests that this occurs not necessarily because of a problem with
the design, but because half of the timing terms are biased by time-varying treatment effects.
ii. Population Weighting
Solon, Haider, and Wooldridge (2015) show that differences between population-weighted (WLS)
and unweighted (OLS) estimates can arise in the presence of unmodeled heterogeneity, and
suggest comparing the two estimators (Deaton 1997, Wooldridge 2001). WLS increases the
34
Grosz, Miller, and Shenhav (2018) propose a similar decomposition for family fixed effects estimates.

24
influence of large units by weighting the means of that make up each 2x2 DD, and it increases
the influence of terms involving large groups by basing the decomposition weights on population
rather than sample shares.
Weighting in the unilateral divorce analysis changes the DD estimate from -3.08 to -0.35. Table
2 indicates that just over half of the difference comes from changes in the 2x2 DD terms, 38 percent
from changes in the weights, and 9 percent from the interaction of the two. Figure 9 scatters the
weighted 2x2 DD’s versus the unweighted ones. Most components do not change and lie along the
45-degree line, but large differences emerge for terms involving the 1970 states: Iowa and
California.
35
Weighting, which obviously gives more influence to California, makes the terms that
use 1970 states as treatments more negative, while it makes terms that use them as controls more
positive. This is consistent either with an ongoing downward trend in suicides in California or, as
discussed above, strongly time-varying treatment effects.
36
iii. Triple-Difference Estimator
When some units should not be (as) affected by a given treatment, they can be used as a
falsification test. Assume that units belong to either an affected group (
= 1) or an unaffected
group (
= 0). The simplest way to incorporate the “third difference”,
, would be to estimate
separate DD coefficients in each sub-sample:
and
. One could equivalently estimate the
35
Lee and Solon (2011) observe that California drives the divergence between OLS and WLS estimate in analyses of
no-fault divorce on divorce rates (Wolfers 2006).
36
Weighting by (a function of) the estimated propensity score (Abadie 2005) is often used to impose covariate balance
between treated and untreated units (see Bailey and Goodman-Bacon 2015). The decomposition theorem points to
two limitations of this approach. First, reweighting untreated observations has no effect on the timing terms. Second,
reweighting untreated observations using the estimated probability of being in any treatment group does not impose
covariate balance within each pair. By changing the relative weight on different untreated units but leaving their total
weight the same, this strategy does not change , so all differences stem from the way reweighting affects the
terms. Table 2 estimates reweighted models based on a propensity score equation that contains the 1960 sex ratio and
per-capita income from figure 8, as well as the 1960 general fertility rate and infant mortality rate. This puts much
more weight on Delaware and less weight on New York, and makes almost all
much less negative, changing the
overall DD estimate to 1.04. Callaway and Sant'Anna (2018) propose a generalized propensity score reweighted
estimator for DD models with timing variation.

25
following triple-difference model (DDD) on the pooled sample including interactions of
with
all variables from equation (2):
37
=
+
+
+
+
+
(19)
is the two-way fixed effects DD estimate for the
= 0 sample and
equals the
difference between the sub-sample DD coefficients:
.
One problem with this estimator is that
equals an average weighted by the cross-
sectional distribution in the in the
= 1 sample, but
uses the cross-sectional distribution of
the
= 0 sample. If
were an indicator for black respondents, then 2x2 DD’s that included
Southern states would get more weight in the black than the white sample while the opposite would
be true for Vermont and New Hampshire. Estimates of (19) difference out cross-state/cross-year
changes in white outcomes weighted by white populations, and so may not capture relative trends
by race within states. A null result for
, which is typically reassuring, could be driven by
completely different 2x2 DD’s than the ones that matter most for
.
DDD specifications that include a more saturated set of fixed effects overcome this
problem. If treatment rolled out by state (), for example, a DDD model can include state-by-time
fixed effects (
):
=
+
+
+
+
+
(20)
The DDD estimate from (20) does equal a weighted average of 2x2 DD’s.
is equivalent to
first collapsing the data to mean differences between -groups within (, ) cells,
,
then estimating a DD model weighted by cell sizes times the
(
|,
)
=
(
1
)
, where
37
In this set up the third difference partitions units, so
is collinear with
.

26
is the mean of
by and . Unlike (19), estimates from (20) do net out changes across
within state/year cells. This changes the weights, though, because the introduction of variation
across the third difference within a cell leads to the typical OLS result that cells with more variation
get more weight. In this case, “more variation” in sample membership within a cell means
approximately equal numbers of units with
= 1 and
= 0.
38
Recasting this version of a DDD model as a DD on differences by
implies that the DD
decomposition theorem holds, albeit with a slight change to the calculation of the weights. All the
results and diagnostic tools derived above apply to specifications like (20) by defining the outcome
as
and using the proper weights.
iv. Unit-specific linear time trends
Researchers control for unit-specific linear time trends to allow “treatment and control states to
follow different trends” (Angrist and Pischke 2009, p 238), and view it as “an important check on
the causal interpretation of any set of regression DD estimates” (Angrist and Pischke 2015, p. 199).
Appendix B derives a closed-form solution for the detrended estimator and shows that a version
of the DD decomposition theorem applies to it. The specific way that unit-specific trends change
each 2x2 component fit with previous intuition. They essentially subtract the cross-group
difference in averages of before and after the middle of the panel,
, but these differences are
weighted by absolute distance to
:
|
|
. This is, as Lee and Solon (2011) point out, akin to a
regression discontinuity design in that the estimator relies less on variation at the beginning or end
of the panel because this variation is absorbed by the trends. Unfortunately, trends tend to absorb
time-varying treatment effects that are necessarily larger at the end of the panel, and in these cases
38
Collapsing the data to the within-cell mean differences
and running OLS on the aggregated data (or
WLS using cell populations) would eliminate the
(
1
)
from the decomposition weights.

27
they over control. Unit-specific trends also increase the weight on units treated at the extremes of
the panel, changing estimates for this reason as well.
The unilateral divorce analysis provides a striking illustration of how unit-specific trends
can fail because figure 5 shows no pre-trends but strongly time-varying treatment effects. Trends
shrink the estimate so much that its sign changes (0.59, s.e.=1.35). Table 2 shows that changes in
2x2 DD’s account for 90 percent of the difference between estimates with and without trends, and
panel A of figure 10 shows that most of the treated/untreated components are much less negative
with trends, with especially large differences for the terms involving the 1970 states. Panel B of
figure 10 shows that trends reduce the weight on
terms, and increase the importance of
timing-only comparisons. Since equation (11c) shows that the timing-only terms are already biased
by the time-varying treatment effects, the change in weighting induced by unit-specific trends
exacerbates this bias, accounting for 47 percent of the coefficient difference. Because unit-specific
trends change the treated/untreated terms and give them less weight, the interaction of those two
factors accounts for -36 percent of the overall change in the estimates.
v. Group-specific linear pre-trends
A simple strategy to address counterfactual trends is to estimate pre-treatment trends in
directly
and partial them out of the full panel (cf. Bhuller et al. 2013, Goodman-Bacon 2018). This is what
we hope that unit-specific trends do, it does not depend on the treatment effect pattern, and it does
not change the weighting of the 2x2 DD’s. Specifically, using data from before
, one can estimate
a pre-trend in
for each timing group.
39
The slope will equal the linear component of
39
One could estimate pre-trends for each unit, but this yields identical point estimates to the group-specific pre-trends.
Moreover, group-specific trends reduce the variability of the estimator because trend deviations that would bias unit
specific pre-trends cancel out to some extent when averaged by timing group. This matters because this strategy
extrapolates potentially many periods into the future, magnifiying specification error in the pre-trends. This point
applies to unit-specific linear trend specifications as well. Point estimates are identical when this specification includes
linear trends for each group rather than each unit.
28
unobservables plus a linear approximation to trend deviations before before
. Removing this
trend from the full panel yields an outcome variable that is robust to linear trends, unaffected by
time-varying treatment effects, and weights each 2x2 DD component in the same way as the
unadjusted estimator. Like the unit-specific time trend control strategy, group-specific pre-trends
are sensitive to non-linear unobservables in the pre-period. Appendix C analyzes this estimator in
detail. Partialling out pre-trends yields a unilateral divorce effect of -6.52 (s.e. = 1.7); close to the
average post-treatment effect of -4.92. While inference is outside the scope of this paper (see Athey
and Imbens 2018), note that this two-step strategy necessarily involves a partly estimated outcome
variable so second-stage standard errors are incorrect.
vi. Disaggregated time effects
If counterfactual outcomes evolve differently by a category, , to which units belong, one can
model these changes flexibly by including separate time fixed effects for each category:
=
+
()
+
×
+
(21)
The coefficient
×
equals an average of two-way fixed effects estimates by values of weighted
by the share of units in each (
) and the within- variance of
. For simplicity, I refer to
as “region”, but the analysis is not specific to region-by-time fixed effects. When treatments vary
by county or city, for example, studies include state-by-time fixed effects (e.g. Almond, Hoynes,
and Schanzenbach 2011, Bailey and Goodman-Bacon 2015); when treatments vary by firm studies
include industry-by-year fixed effects (e.g. Kovak, Oldenski, and Sly 2018).
Since the decomposition theorem holds for each within-region DD estimate, it also holds
for
×
. Each 2x2 DD averages the region-specific 2x2 DD’s (
,
and
,
) but the weights
reflect region size and the within-region distribution of timing groups:

29
,×
=
,
(22)
,×
=
,×
,
+ (1
)
,×
,
(23)
2x2 DD’s from large regions get more weight (via the
), but the distribution of timing groups
within region (the
terms) also determine the importance of each region. Regions with no
units in group contribute nothing to 2x2 DD’s involving that group, in contrast to the simpler
estimator where that region would contribute controls for group . If no region contains units from
a given pair of groups that pair drops out of the disaggregated time effects specification. These
within-region 2x2 DD’s in (22) and (23) are weighted together using the cross-region average of
the sample share products,
as well as treatment variances.
Adding region-by-year effects to the unilateral divorce analysis cuts the estimated effect by a
factor of three (-1.16). Figure 11 plots the 2x2 DD’s and the weights from this specification against
those from the baseline model. 43 of the 156 2x2 terms in the baseline model drop out of the
within-region specification, and table 2 shows that about three quarters of the difference in the
estimates comes from the way these fixed effects change the weights.
IV. CONCLUSION
Difference-in-differences is perhaps the most widely applicable quasi-experimental research
design. Its transparency makes it simple to describe, test, interpret, and teach. This paper extends
all of these advantages from canonical two-by-two DD models to general and much more common
DD models with variation in the timing of treatment.
My central result, the DD decomposition theorem, shows that a two-way fixed effects DD
coefficient equals a weighted average of all possible simple 2x2 DD’s that compare one group that
changes treatment status to another group that does not. Many ways in which the theoretical
30
interpretation of regression DD differs from the canonical model stem from the fact that these
simple components are weighted together based both on sample sizes and the variance of their
treatment dummy. This defines the DD estimand, the variance-weighted average treatment effect
on the treated (VWATT), and generalizes the identifying assumption on counterfactual outcomes
to variance-weighted common trends (VWCT). Moreover, I show that because already-treated
units act as controls in some 2x2 DD’s, the two-way fixed effects model requires an additional
identifying assumption of time-invariant treatment effects.
The DD decomposition theorem also leads to several new tools for practitioners. Graphing
the 2x2 DD’s against their weight displays all the identifying variation in any DD application, and
summing weights across types of comparisons quantifies “how much” of a given estimate comes
from different sources of variation. I use the DD decomposition theorem to propose a reweighted
balance test that reflects this identifying variation, is easy to implement, has higher power than
tests of joint balance across groups, and shows how large and in what direction any imbalance
occurs. I suggest several simple methods to learn why estimates differ across alternative
specifications. The weighted average representation leads to a Oaxaca-Blinder-Kitagawa-style
decomposition that quantifies how much of the difference in estimates comes from changes in the
2x2 DD’s, the weights, or both. Plots of the components or the weights across specifications show
clearly where differences come from and can help researchers understand why their estimates
changes and whether or not it is a problem.

31
Figure 1. Difference-in-Differences with Variation in Treatment Timing: Three Groups
Notes: The figure plots outcomes in three groups: a control group, , which is never treated; an early treatment group,
, which receives a binary treatment at
=
34
100
; and a late treatment group, , which receives the binary treatment
at
=
85
100
. The x-axis notes the three sub-periods: the pre-period for group , [1,
1], denoted by (); the
middle period when group is treated and group is not, [
,
1], denoted by (, ); and the post-period for
group , [
, ], denoted by (). I set the treatment effect to 10 in group and 15 in group .
t*
l
t*
k
y
k
it
y
l
it
y
U
it
MID(k,l)PRE(k) POST(l)
0 10 20 30 40
Units of y
Time

32
Figure 2. The Four Simple (2x2) Difference-in-Differences Estimates from the Three Group
Case
Notes: The figure plots the groups and time periods that generate the four simple 2x2 difference-in-difference
estimates in the case with an early treatment group, a late treatment group, and an untreated group from Figure 1. Each
panel plots the data structure for one 2x2 DD. Panel A compares early treated units to untreated units (
); panel B
compares late treated units to untreated units (
); panel C compares early treated units to late treated units during
the late group’s pre-period (
,
); panel D compares late treated units to early treated units during the early group’s
post-period (
,
). The treatment times mean that
= 0.67 and
= 0.16, so with equal group sizes, the
decomposition weights on the 2x2 estimate from each panel are 0.365 for panel A, 0.222 for panel B, 0.278 for panel
C, and 0.135 for panel D.
t*
k
y
k
it
y
U
it
PRE(k) POST(k)
0 10 20 30 40
Units of y
Time
A. Early Group vs. Untreated Group
t*
l
y
l
it
y
U
it
PRE(l) POST(l)
0 10 20
30 40
Units of y
Time
B. Late Group vs. Untreated Group
t*
l
t*
k
y
k
it
y
l
it
MID(k,l)PRE(k)
0 10 20 30 40
Units of y
Time
C. Early Group vs. Late Group, before t*
l
t*
l
t*
k
y
k
it
y
l
it
MID(k,l) POST(l)
0
10
20 30
40
Units of y
Time
D. Late Group vs. Early Group, after t*
k

33
Figure 3. Difference-in-Differences Estimates with Variation in Timing Are Biased When
Treatment Effects Vary Over Time
Notes: The figure plots a stylized example of a timing-only DD set up with a treatment effect that is a trend-break
rather than a level shift (see Meer and West 2013). Following section II.A.ii, the trend-break effect equals (
+ 1). The top of the figure notes which event-times lie in the (), (, ), and () periods for each
unit. The figure also notes the average difference between groups in each of these periods. In the
(, ) pe
riod,
outcomes differ by
2
(
+ 1
)
on average. In the () period, however, outcomes had already been growing
in the early group for
periods, and so they differ by
(
+ 1
)
on average. The 2x2 DD that compares
the later group to the earlier group is biased and, in the linear trend-break case, weakly negative despite a positive and
growing treatment effect.
t*
l
t*
k
φ
(t*
l
-t*
k
+1)/2
φ
(t*
l
-t*
k
+1)
k
event times: [0, (
t*
l
-
t*
k
)-1]
l
event times: [-(
t*
l
-
t*
k
), -1]
k
event times: [-(
t*
k
-1
), -1]
l
event times: [-(
t*
l
-1
), -(
t*
l
-
t*
k
)-1]
k
event times: [(
t*
l
-
t*
k
), T-
t*
k
]
l
event times: [0, T-
t*
l
]
0 50 100 150
Units of y
Time

34
Figure 4. Weighted Common Trends: The Treatment/Control Weights as a Function of the
Share of Time Spent Under Treatment
Notes: The figure plots the weights that determine each timing group’s importance in the weighted common trends
expression in equations (16) and (17).
Treatment-Control
Weight
Treatment-Control Weight,
Timing Only
0
Weight for Each Treatment Group
0 .2 .4 .6
.8
1
Treatment Time/Total Time
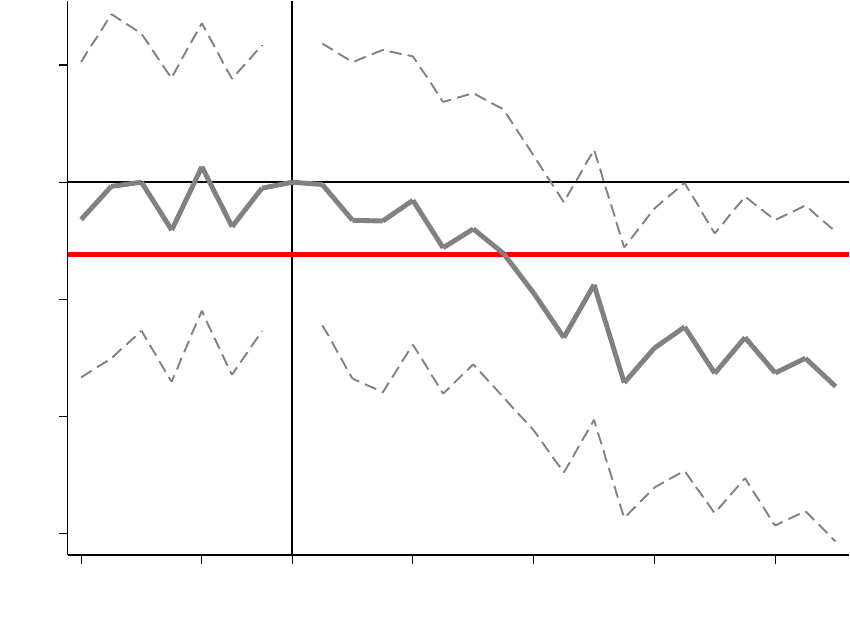
35
Figure 5. Event-Study and Difference-in-Differences Estimates of the Effect of No-Fault
Divorce on Female Suicide: Replication of Stevenson and Wolfers (2006)
Notes: The figure plots event-study estimates from the two-way fixed effects model on page 276 and plotted in figure
1 of Stevenson and Wolfers (2006), along with the DD coefficient. The specification does not include other controls
and does not weight by population. Standard errors are robust to heteroskedasticity.
DD Coefficient = -3.08 (s.e. = 1.27)
-15 -10
-5 0 5
Suicides per 1m women
-8
-4 -1
3
7
11
15
Years Relative to Divorce Reform

36
Figure 6. Difference-in-Differences Decomposition for Unilateral Divorce and Female
Suicide
Notes: Notes: The figure plots each 2x2 DD components from the decomposition theorem against their weight for the
unilateral divorce analysis. The open circles are terms in which one timing group acts as the treatment group and the
pre-1964 reform states act as the control group. The closed triangles are terms in which one timing group acts as the
treatment group and the non-reform states act as the control group. The x’s are the timing-only terms. The figure notes
the average DD estimate and total weight on each type of comparison. The two-way fixed effects estimate, -3.08,
equals the average of the y-axis values weighted by their x-axis value.
DD Estimate = -3.08
Later Group Treatment vs. Earlier Group Control
Weight = 0.26; DD = 3.51
Earlier Group Treatment vs. Later Group Control
Weight = 0.11; DD = -0.19
Treatment vs. Non-Reform States
Weight = 0.24; DD = -5.33
Treatment vs. Pre-1964 Reform States
Weight = 0.38; DD = -7.04
-30 -20 -10 0
10 20 30
2x2 DD Estimate
0
.02
.04
.06
.08
.1
Weight

37
Figure 7. Weighted Common Trends in the Unilateral Divorce Analysis: The
Treatment/Control Weights on Each Timing Group
Notes: The figure plots the weights that determine each timing group’s role in the weighted common trends expression.
These are show in solid triangles and equal the difference between the total weight each treatment timing group
receives in terms where it is the treatment group (
) and terms where it is the control group (
):
. The
solid circles show the same weights but for versions of each estimator that exclude the untreated (or already-treated)
units and, therefore, are identified only by treatment timing. The open squares plot each group’s sample share.
Sample Share
Treatment-Control Weight
Treatment-Control Weight, Timing-Only
-.1 0 .1 .2 .3
Weight for Each Treatment Group
1970 1975 1980 1985
Treatment Time
f ( )

38
Figure 8. Testing for Balance in a Difference-in-Differences Model with Timing:
Reweighted Test versus Joint Test
Notes: The figure plots average per-capita income and male/female sex ratio in 1960 for each timing group in the
unilateral divorce analysis (combining the non-reform and pre-1964 reform states into the group labeled “Pre-64 +
NRS”). The horizontal lines equal the average of these variables using the weights from figure 6 (
). Note
that the 1969 states get more weight as a control group, so they are part of the reweighted control mean. Each panel
reports the F-statistic and p-value from a joint test of equality across the means, and the reweighted difference,
standard error, and p-value from the re-weighted balance test. The top of the figure reports
2
() test-statistics for
both covariates estimated using seemingly unrelated regressions.
Joint F-Stat:
0.89 (p-val = 0.56)
Reweighted Diff:
2285, s.e. = 835
(p-val = 0.01)
5000
10000
13418
15703
20000
25000
Per-Capita Income, $2014
Pre-64 + NRS
1969
1970
1971
1972
1973
1974
1975
1976
1977
1980
1984
1985
A. 1960 Per-Capita Income
Joint F-Stat:
1.10 (p-val = 0.39)
Reweighted Diff:
0.02, s.e. = 0.01
(p-val = 0.06)
.8
.9
.98
.96
1.1
Age-Adjusted M/F Sex Ratio, 15-44
Pre-64 + NRS
1969
1970
1971
1972
1973
1974
1975
1976
1977
1980
1984
1985
B. 1960 M/F Sex Ratio
Joint Test by Group:
χ
2
(24)=23.8 (p-val = 0.47)
Joint Test of Reweighted Differences:
χ
2
(2) =11.1 (p-val = 0.00)
Reweighted Treatment Mean Reweighted Control Mean
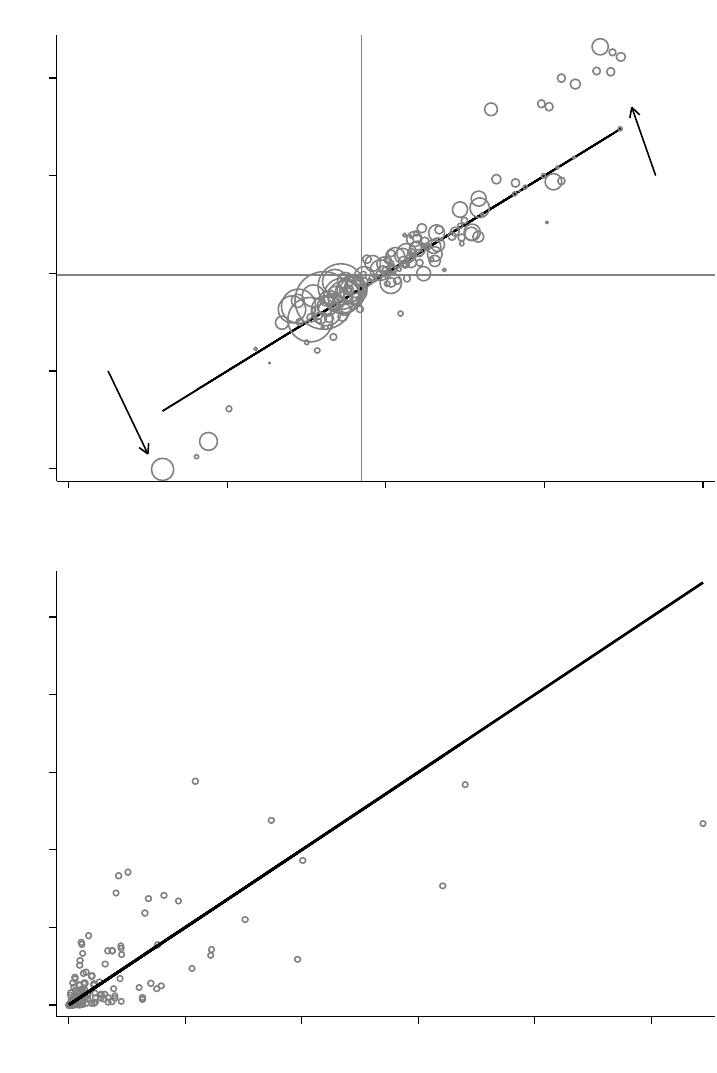
39
Figure 9. Comparison of 2x2 DD Components and Decomposition Weights with and
without Population Weights
Notes: Panel A plots the 2x2 DD components from two-way fixed effects estimates that use population weights (y-
axis) and do not (x-axis). The size of each point is proportional to its weight in an OLS version of equation (7). WLS
estimates are much smaller than OLS estimates, and this figure shows that the source of this discrepancy is the 1970
no-fault divorce states, which include only Iowa and California. Weighting puts much more emphasis on California
and, therefore, every 2x2 DD component involving the 1970 states. Dropping California changes yields an OLS
estimate of -3.32 and a WLS estimate of -1.43.
1970 v 1969
1970 v 1971
1970 v 1972
1970 v 1973
1970 v 1974
1970 v 1975
1970 v 1976
1970 v 1977
1970 v 1980
1970 v 1984
1970 v 1985
1970 v NRS
1970 v PRE
1969 v 1970
1971 v 1970
1972 v 1970
1973 v 1970
1974 v 1970
1975 v 1970
1976 v 1970
1977 v 1970
1980 v 1970
1984 v 1970
1985 v 1970
1970 States are
the Control
1970 States are
the Treatment
WLS = -0.35
OLS = -3.08
-40 -20 0 20 40
Weighted 2x2 DDs
-40 -20 0 20 40
Unweighted 2x2 DDs
A. 2x2 DD's
0 .02 .04 .06 .08 .1
Decomposition weights, WLS
0 .02 .04 .06 .08 .1
Decomposition weights, OLS
B. 2x2 Weights

40
Figure 10. Comparison of 2x2 DD Components and Decomposition Weights with and
without Unit-Specific Linear Time Trends
Notes: Panel A plots the two-group DD’s from a model with unit-specific time trends (y-axis) against those from a
model without trends (x-axis). The size of each point is proportional to its weight in a model without trends. The trend-
adjusted estimate is small and positive compared to a negative DD estimate without them. Much of the change comes
from the effect of trends on each 2x2 estimate, especially for treated/untreated comparisons (closed triangles). Panel
B is the same except that it plots the weights. Treated/untreated terms that received the most weight in the unadjusted
model get relatively less in a trend-adjusted model. Timing terms that received more weight get relatively more in a
trend-adjusted model.
1970 v NRS
1970 v PRE
DDs w/ trends = 0.59
DDs w/out trends = -3.08
-30 -20 -10 0 10 20 30
2x2 DDs w/ trends
-30
-20
-10
0
10
20
30
2x2 DDs w/out trends
Timing Estimates
Treated/Untreated Estimates
A. 2x2 DD's
0 .02 .04 .06 .08 .1
Decomposition weights w/ trends
0
.02
.04
.06
.08
.1
Decomposition weights w/out trends
Timing Estimates
Treated/Untreated Estimates
B. 2x2 Weights

41
Figure 11. Comparison of 2x2 DD Components and Decomposition Weights with and
without Region-by-Year Fixed Effects
Notes: Panel A plots the two-group DD’s from a model with region-by-year fixed effects (y-axis) against those from
a model without them (x-axis). The size of each point is proportional to its weight in the sparser model with only year
fixed effects. 2x2 DD’s that drop out of the region-by-year FE model are shown in triangles and appear at “0” on the
y-axis, although they do not enter the decomposition as zeros. Panel B plots the decomposition weights from the two
models. Some 2x2 comparisons drop out in the model with region-by-year effects (when no region has states from
both timing groups) and the figures plot these components using triangles.
Region-by-
Year FE = -1.16
OLS = -3.08
-50 0 50
2x2 DDs, Region-by-Year FE
-40 -20
0 20
40
2x2 DDs, Year FE
2x2 DD's in both estimators
2x2 DD's that drop out
with region-by-year FE
A. 2x2 DD's
0 .02 .04 .06 .08 .1
Decomposition weights w/ Region-by-Year FE
0 .02 .04 .06 .08 .1
Decomposition weights w/ Year FE
2x2 DD's in both estimators
2x2 DD's that drop out
with region-by-year FE
B. 2x2 Weights

42
Table 1. The No-Fault Divorce Rollout: Treatment Times, Group Sizes, and Treatment
Shares
No-Fault Divorce
Year (
)
Number of
States
Share of
States (
)
Treatment Share
(
)
Non-Reform States
5
0.10
.
Pre-1964 Reform States
8
0.16
.
1969
2
0.04
0.85
1970
2
0.04
0.82
1971
7
0.14
0.79
1972
3
0.06
0.76
1973
10
0.20
0.73
1974
3
0.06
0.70
1975
2
0.04
0.67
1976
1
0.02
0.64
1977
3
0.06
0.61
1980
1
0.02
0.52
1984
1
0.02
0.39
1985
1
0.02
0.36
Notes: The table lists the dates of no-fault divorce reforms from Stevenson and Wolfers (2006), the number and share
of states that adopt in each year, and the share of periods each treatment timing group spends treated in the estimation
sample from 1964-1996.

43
Table 2. DD Estimates of the Effect of Unilateral Divorce Analysis on Female Suicide using
Alternative Specifications
(1)
(2)
(3)
(4)
(5)
(6)
(7)
Baseline
No
Untreated
States
WLS
Propensity
Score
Weighting
Unit-
Specific
Trends
Group-
Specific
Pre-
Trends
Region-
by-Year
Fixed
Effects
Unilateral Divorce
-3.08
2.42
-0.35
1.04
0.59
-6.52
-1.16
[1.27]
[1.81]
[1.97]
[1.78]
[1.35]
[2.98]
[1.37]
Difference from
baseline
specification
5.50 2.73 4.12 3.67 -3.44 1.92
Share due to:
2x2 DDs
0
0.52
1
0.90
1
0.37
Weights
1
0.39
0
0.47
0
0.76
Interaction
0
0.09
0
-0.36
0
-0.13
Notes: The table presents DD estimates from the alternative specifications discussed in section III. Column (1) is the
two-way fixed effects estimate from equation (2). Column (2) drops the pre-1964 reform and non-reform states.
Column (3) weights by state adult populations in 1964. Column (4) weights by the inverse propensity score estimated
from a probit model that contains the sex ratio, per-capita income, the general fertility rate, and the infant mortality
rate all measured in 1960. Column (5) includes state-specific linear time trends. Column (6) comes from a two-step
procedure that first estimates group-specific trends from 1964-1968, subtracts them from the suicide rate, and
estimates equation (2) on the transformed outcome variable. Column (7) includes region-by-year fixed effects. Below
the standard errors I show the difference between each estimate and the baseline result, an the last three rows show
the share of this difference that comes from changes in the 2x2 DD’s, the weights, or their interaction as shown in
equation (18).

44
V. REFERENCES
Abadie, Alberto. 2005. "Semiparametric Difference-in-Differences Estimators." The Review of Economic Studies
72 (1):1-19.
Abadie, Alberto, Alexis Diamond, and Jens Hainmueller. 2010. "Synthetic Control Methods for Comparative Case
Studies: Estimating the Effect of California’s Tobacco Control Program." Journal of the American
Statistical Association 105 (490):493-505. doi: 10.1198/jasa.2009.ap08746.
Abraham, Sarah, and Liyang Sun. 2018. "Estimating Dynamic Treatment Effects in Event Studies with
Heterogeneous Treatment Effects." Working Paper.
Allcott, Hunt. 2015. "Site Selection Bias in Program Evaluation." The Quarterly Journal of Economics 130
(3):1117-1165. doi: 10.1093/qje/qjv015.
Almond, Douglas, Hilary W. Hoynes, and Diane Whitmore Schanzenbach. 2011. "Inside the War On Poverty: The
Impact of Food Stamps on Birth Outcomes." The Review of Economics and Statistics 93 (2):387-403. doi:
10.2307/23015943.
Angrist, Joshua D. 1988. "Grouped Data Estimation and Testing in Simple Labor Supply Models." Princeton
University Working Paper.
Angrist, Joshua D. 1991. "Grouped-data estimation and testing in simple labor-supply models." Journal of
Econometrics 47 (2):243-266. doi: https://doi.org/10.1016/0304-4076(91)90101-I
.
Angrist, Joshua D., and Alan B. Krueger. 1999. "Chapter 23 - Empirical Strategies in Labor Economics." In
Handbook of Labor Economics, edited by Orley C. Ashenfelter and David Card, 1277-1366. Elsevier.
Angrist, Joshua David, and Jörn-Steffen Pischke. 2009. Mostly harmless econometrics : an empiricist's companion.
Princeton: Princeton University Press.
Angrist, Joshua David, and Jörn-Steffen Pischke. 2015. Mastering 'metrics : the path from cause to effect. Princeton
; Oxford: Princeton University Press.
Athey, Susan, and Guido W. Imbens. 2006. "Identification and Inference in Nonlinear Difference-in-Differences
Models." Econometrica 74 (2):431-497.
Athey, Susan, and Guido W. Imbens. 2018. "Design-based Analysis in Difference-in-Differences Settings with
Staggered Adoption." Working Paper.
Bailey, Martha J., and Andrew Goodman-Bacon. 2015. "The War on Poverty's Experiment in Public Medicine:
Community Health Centers and the Mortality of Older Americans." American Economic Review 105
(3):1067-1104.
Bertrand, Marianne, Esther Duflo, and Sendhil Mullainathan. 2004. "How Much Should We Trust Differences-In-
Differences Estimates?" The Quarterly Journal of Economics 119 (1):249-275.
Besley, Timothy, and Anne Case. 2002. "Unnatural Experiments? Estimating the Incidence of Endogenous
Policies." The Economic Journal 110 (467):672-694. doi: 10.1111/1468-0297.00578.
Bhuller, Manudeep, Tarjei Havnes, Edwin Leuven, and Magne Mogstad. 2013. "Broadband Internet: An
Information Superhighway to Sex Crime?" The Review of Economic Studies 80 (4 (285)):1237-1266.
Bitler, Marianne P., Jonah B. Gelbach, and Hilary W. Hoynes. 2003. "Some Evidence on Race, Welfare Reform,
and Household Income." The American Economic Review 93 (2):293-298. doi: 10.2307/3132242.
Blinder, Alan S. 1973. "Wage Discrimination: Reduced Form and Structural Estimates." The Journal of Human
Resources 8 (4):436-455. doi: 10.2307/144855.
Borusyak, Kirill, and Xavier Jaravel. 2017. "Revisiting Event Study Designs." Harvard University Working Paper.
Callaway, Brantly, Tong Li, and Tatsushi Oka. forthcoming. "Quantile Treatment Effects in Difference in
Differences Models under Dependence Restrictions and with only Two Time Periods." Journal of
Econometrics.
Callaway, Brantly, and Pedro Sant'Anna. 2018. "Difference-in-Differences With Multiple Time Periods and an
Application on the Minimum Wage and Employment." Working Paper.
Cameron, Adrian Colin, and P. K. Trivedi. 2005. Microeconometrics : methods and applications. Cambridge ; New
York: Cambridge University Press.
Chernozhukov, Victor, Iván Fernández‐Val, Jinyong Hahn, and Whitney Newey. 2013. "Average and Quantile
Effects in Nonseparable Panel Models." Econometrica 81 (2):535-580. doi: 10.3982/ECTA8405.
Chyn, Eric. forthcoming. "Moved to Opportunity: The Long-Run Effect of Public Housing Demolition on Labor
Market Outcomes of Children." American Economic Review.
de Chaisemartin, C., and X. D’HaultfŒuille. 2018a. "Fuzzy Differences-in-Differences." The Review of Economic
Studies 85 (2):999-1028. doi: 10.1093/restud/rdx049.

45
de Chaisemartin, C.;, and X. D’HaultfŒuille. 2018b. "Two-way fixed effects estimators with heterogeneous
treatment effects." Working Paper.
Deaton, Angus. 1997. The Analysis of Household Surveys : a Microeconometric Approach to Development Policy.
Baltimore, MD: Johns Hopkins University Press.
Deshpande, Manasi, and Yue Li. 2017. "Who Is Screened Out? Application Costs and the Targeting of Disability
Programs." National Bureau of Economic Research Working Paper Series No. 23472. doi:
10.3386/w23472.
Fadlon, Itzik, and Torben Heien Nielsen. 2015. "Family Labor Supply Responses to Severe Health Shocks."
National Bureau of Economic Research Working Paper Series No. 21352. doi: 10.3386/w21352.
Freyaldenhoven, Simon, Christian Hansen, and Jesse M. Shapiro. 2018. "Pre-event Trends in the Panel Event-study
Design." National Bureau of Economic Research Working Paper Series No. 24565. doi: 10.3386/w24565.
Frisch, Ragnar, and Frederick V. Waugh. 1933. "Partial Time Regressions as Compared with Individual Trends."
Econometrica 1 (4):387-401. doi: 10.2307/1907330.
Gibbons, Charles, E., Juan Carlos Suárez Serrato, and Michael Urbancic, B. 2018. Broken or Fixed Effects? In
Journal of Econometric Methods.
Goodman-Bacon, Andrew. 2018. "The Long-Run Effects of Childhood Insurance Coverage: Medicaid
Implementation, Adult Health, and Labor Market Outcomes." Working Paper.
Goodman, Joshua. 2017. "The Labor of Division: Returns to Compulsory High School Math Coursework."
National Bureau of Economic Research Working Paper Series No. 23063. doi: 10.3386/w23063.
Grosz, Michael, Douglas L. Miller, and Na'ama Shenhav. 2018. "All In the Family: Assessing the External Validity
of Family Fixed Effects Estimates and the Long Term Impact of Head Start." Working Paper.
Haines, Michael R., and ICPSR. 2010. Historical, Demographic, Economic, and Social Data: The United States,
1790-2002. ICPSR [distributor].
Heckman, James J., Robert J. Lalonde, and Jeffrey A. Smith. 1999. "Chapter 31 - The Economics and Econometrics
of Active Labor Market Programs." In Handbook of Labor Economics, edited by Orley C. Ashenfelter and
David Card, 1865-2097. Elsevier.
Holland, Paul W. 1986. "Statistics and Causal Inference." Journal of the American Statistical Association 81
(396):945-960. doi: 10.2307/2289064.
Imai, Kosuke, In Song Kim, and Erik Wang. 2018. "Matching Methods for Causal Inference with Time-Series
Cross-Section Data." Working Paper.
Imbens, Guido W., and Joshua D. Angrist. 1994. "Identification and Estimation of Local Average Treatment
Effects." Econometrica 62 (2):467-475. doi: 10.2307/2951620.
Jacobson, Louis S., Robert J. LaLonde, and Daniel G. Sullivan. 1993. "Earnings Losses of Displaced Workers." The
American Economic Review 83 (4):685-709. doi: 10.2307/2117574.
Joseph Hotz, V., Guido W. Imbens, and Julie H. Mortimer. 2005. "Predicting the efficacy of future training
programs using past experiences at other locations." Journal of Econometrics 125 (1):241-270. doi:
https://doi.org/10.1016/j.jeconom.2004.04.009
.
Kitagawa, Evelyn M. 1955. "Components of a Difference Between Two Rates." Journal of the American Statistical
Association 50 (272):1168-1194. doi: 10.2307/2281213.
Kovak, Brian, Lindsay Oldenski, and Nicholas Sly. 2018. "The Labor Market Effects of Offshoring by U.S.
Multinational Firms: Evidence from Changes in Global Tax Policies." Working Paper.
Krolikowski, Pawel. 2017. "Choosing a Control Group for Displaced Workers." ILR Review:0019793917743707.
doi: 10.1177/0019793917743707.
Lee, David S., and Thomas Lemieux. 2010. "Regression Discontinuity Designs in Economics." Journal of
Economic Literature 48 (2):281-355.
Lee, Jin Young, and Gary Solon. 2011. "The Fragility of Estimated Effects of Unilateral Divorce Laws on Divorce
Rates." National Bureau of Economic Research Working Paper Series No. 16773.
Malkova, Olga. 2017. "Can Maternity Benefits Have Long-Term Effects on Childbearing? Evidence From Soviet
Russia." The Review of Economics and Statistics. doi: 10.1162/REST_a_00713.
Meer, Jonathan, and Jeremy West. 2013. "Effects of the Minimum Wage on Employment Dynamics." National
Bureau of Economic Research Working Paper Series No. 19262. doi: 10.3386/w19262.
Meyer, Bruce D. 1995. "Natural and Quasi-Experiments in Economics." Journal of Business & Economic Statistics
13 (2):151-161. doi: 10.2307/1392369.
Neumark, David, J. M. Ian Salas, and William Wascher. 2014. "Revisiting the Minimum Wage—Employment
Debate: Throwing Out the Baby with the Bathwater?" ILR Review 67 (3_suppl):608-648. doi:
10.1177/00197939140670S307.
46
Oaxaca, Ronald. 1973. "Male-Female Wage Differentials in Urban Labor Markets." International Economic Review
14 (3):693-709. doi: 10.2307/2525981.
Oster, Emily. 2016. "Unobservable Selection and Coefficient Stability: Theory and Evidence." Journal of Business
& Economic Statistics:1-18. doi: 10.1080/07350015.2016.1227711.
Pei, Zhuan, Jörn-Steffen Pischke, and Hannes Schwandt. 2017. "Poorly Measured Confounders are More Useful on
the Left Than on the Right." National Bureau of Economic Research Working Paper Series No. 23232.
doi: 10.3386/w23232.
Perron, Pierre. 2006. "Dealing with Structural Breaks." Working Paper.
Rubin, Donald B. 1974. "Estimating causal effects of treatments in randomized and nonrandomized studies."
Journal of Educational Psychology 66 (5):688-701. doi: 10.1037/h0037350.
Shore-Sheppard, Lara D. . 2009. "Stemming the Tide? The Effect of Expanding Medicaid Eligibility On Health
Insurance Coverage." The B.E. Journal of Economic Analysis & Policy 8 (2).
Snow, John. 1855. On the Mode of Communication of Cholera. Edited by John Churchill. Second ed. London.
Solon, Gary, Steven J. Haider, and Jeffrey M. Wooldridge. 2015. "What Are We Weighting For?" Journal of
Human Resources 50 (2):301-316.
Stevenson, Betsey, and Justin Wolfers. 2006. "Bargaining in the Shadow of the Law: Divorce Laws and Family
Distress." The Quarterly Journal of Economics 121 (1):267-288.
Strezhnev, Anton. 2018. "Semiparametric Weighting Estimators for Multi-Period Difference-in-Differences
Designs." Working Paper.
Surveillance, Epidemiology, and End Results (SEER). 2013. Surveillance, Epidemiology, and End Results (SEER)
Program Populations (1969-2011). edited by DCCPS National Cancer Institute, Surveillance Research
Program, Surveillance Systems Branch.
Walters, Christopher R. forthcoming. "The Demand for Effective Charter Schools." Journal of Political Economy.
Wolfers, Justin. 2006. "Did Unilateral Divorce Laws Raise Divorce Rates? A Reconciliation and New Results."
American Economic Review 96 (5):1802-1820.
Wooldridge, Jeffrey M. 2001. "Asymptotic Properties of Weighted M-Estimators for Standard Stratified Samples."
Econometric Theory 17 (2):451-470.
Wooldridge, Jeffrey M. 2005. "Fixed-Effects and Related Estimators for Correlated Random-Coefficient and
Treatment-Effect Panel Data Models." The Review of Economics and Statistics 87 (2):385-390.
Wooldridge, Jeffrey M. 2010. Econometric analysis of cross section and panel data. 2nd ed. Cambridge, Mass.:
MIT Press.
